DIU EIL de Grenoble – bloc 2 : Algorithmique

Retour au site principal du DIU

Table des matières

1. Documents 2020
2. Évaluation 2019
3. Documents 2019
4. Quelques références bibliographiques

1 Documents 2020

Apprentissage Par Problèmes (Lundi 6 juillet)

Les documents distribués :
- APP Généralités
- APP2: Hold'em for n00bs

Débat scientifique (Lundi 6 juillet)

Les deux diapos
- Débat scientifique (principe)
- Débat scientifique: question
Les scripts utilisés pour la séance en fichier zip
Pour compléter la séance :
- Ensembles et Séquences vs Tableaux : sur la représentation des ensembles et séquences en mémoire à base de tableaux (proche de ce qu'utilise python pour ses listes)
- Complexité : une introduction à la complexité algorithmique

Démarche algorithmique et complexité Lundi 6 juillet)

une petite introduction à la démarche algorithmique et la la complexité d'un problème Transparents

Comme exercice on peut analyser les différents algorithmes de calcul des nombres de Fibonnacci Code python

le calcul par appels récursifs, mémoisation explicite (dictionnaire) ou implicite (décoration de fonction)
le calcul itératif (approche bottom-up avec ou sans recouvrement de la mémoire)
une approche matricielle basée sur l'exponentiation rapide de matrice
reprendre avec le schéma du TD de programmation \[\begin{cases} F_{2n}=F_n^2+F_{n-1}^2 & \\ F_{2n+1}= (2F_{n-1}+F_n)F_n& \end{cases}\]

Bien entendu les méthodes de comptage et de mesure de temps d'exécution sont rudimentaires, il est plus intéressant d'utiliser des décorateurs de fonctions qui ajouteront automatiquement la fonctionalité demandée et sera donc réutilisable dans tout contexte.

On peut également reprendre la formule de Binet en utilisant l'exponentiation rapide et un arrondi. \[ F_n=\frac 1 {\sqrt{5}} \left( \frac {1+\sqrt{5}}2\right)^{n+1} - \frac 1 {\sqrt{5}} \left( \frac {1-\sqrt{5}}2\right)^{n+1} \]

Comment évolue la taille de \(F_n\) en fonction de \(n\) ? Quelles remarques peut-on faire sur la complexité du calcul ?

Introduction aux preuves de correction et de terminaison de programmes (mardi 7 juillet)

Transparents

Un code sans bug, c'est parfois impératif (nucléaire, aviation, etc.) Les tests sont un élément essentiel du développement logiciel permettant de détecter et corriger des bugs (le plus tôt est le mieux), mais ils ne suffisent pas dans certains contextes.

Pour prouver (mais aussi pour tester), il faut avoir des spécifications (plus ou moins formelles) comme les signatures (des modules, objets, fonctions, etc.), les pré-conditions, les post-conditions, etc.

Pour les algorithmes, on peut prouver différents types de propriétés (terminaison, complexité, correction, etc.), preuves communes ou séparées suivant les algorithmes. Comme en mathématique, les preuves peuvent être plus ou moins formelles. En cas de boucles dans les algorithmes, les preuves utilisent souvent la notion d'invariants (propriétés vérifiées à chaque tour de boucle). Trouver le bon invariant est souvent la partie difficile de la preuve.

Une preuve n'est valide que dans son contexte. Une preuve d'un algorithme ne suffit pas à garantir un programme sans bug. Il faut aussi qu'il n'y ait pas de bugs dans l'implémentation de l'algorithme (dans le langage choisi par le programmeur), ni dans les outils de compilation, ni dans l'environnement de programmation et d'exécution (bibliothèques, système d'exploitation, etc.), ni dans le matériel exécutant le code (microprocesseurs, bus de communication, etc.), ni …

Exemple avec des algorithmes de tris et une correction plutôt formelle de la preuve du tri par insertion. Fichier python des algorithmes de tris proposés.

Apprentissage Par Problèmes (Mardi 7 juillet + suite)

Les documents distribués :
- APP2: Hold'em for n00bs
Les documents supplémentaires :

Diviser pour régner

pour le Tri partition/fusion et le quicksort voir les feuilles de TD (le niveau est à adapter à des terminales, les TD vont au-dela)

Pour le Master theorem (savoir qu'il existe et qu'il y a 3 cas de figure)

voir les documents en fin de page sur les enveloppes convexes

Structures arborescentes

Cours (Jeudi 24 septembre 2020)
Exercices (Vendredi 25 septembre 2020)
- comptage et parcours d'arbres binaires (sujet, corrigé)
- manipulation d'arbres binaires (sujet, corrigé)
- manipulation d'arbres n-aires (sujet, corrigé)
- dictionnaire arborescent (sujet, corrigé)

Introduction aux graphes par Nadia Brauner

Transparents

Recherche de motifs dans un texte

Transparents

Structure de donnée partition : Union-Find

Les transparents ici

Algorithmes glouton

Les transparents et le problème de l'allocation d'intervalles (code illustratif, non optimisé)

Arbre couvrant minimal : Kruskal-Prim

Transparents du cours
Fiche de TD

2 Évaluation 2019

Cette évaluation se déclinera en trois points :

Un QCM de 3/4 d'heure qui sera fait le vendredi 28 juin matin pendant une séance d'algorithmique, et qui portera sur les notions vues en séances jusqu'à ce jour.
Un rapport à effectuer par groupes de 5-6 personnes et qui portera sur un problème que vous aurez à étudier durant 4 séances d'Apprentissage Par Problème (APP). Ce rapport pourra être effectué sous forme électronique ou papier.
La fiche d'activité (séquence pédagogique), comme dans les autres blocs.

Les rendus sont pour le vendredi 5 juillet, à donner en main propre ou envoyer aux personnes suivantes : Florent Bouchez Tichadou, Jean-Marc Vincent, Vincent Danjean.

N'hésitez pas à nous contacter si vous souhaitez plus de précisions.

3 Documents 2019

Débat scientifique (Jeudi 11 avril)

Les deux diapos
- Débat scientifique (principe)
- Débat scientifique: question
Les scripts utilisés pour la séance en fichier zip
Pour compléter la séance :
- Ensembles et Séquences vs Tableaux : sur la représentation des ensembles et séquences en mémoire à base de tableaux (proche de ce qu'utilise python pour ses listes)
- Complexité : une introduction à la complexité algorithmique

Introduction aux preuves de correction et de terminaison de programmes (Mercredi 15 mai et mercredi 22 mai)

Exemple avec des algorithmes de tris et une correction plutôt formelle de la preuve du tri par insertion. Fichier python des algorithmes de tris proposés.

Démarche algorithmique et complexité (Mercredi 22 mai)

une petite introduction à la démarche algorithmique et la la complexité d'un problème Transparents

Comme exercice on peut analyser les différents algorithmes de calcul des nombres de Fibonnacci Code python

le calcul par appels récursifs, mémoisation explicite (dictionnaire) ou implicite (décoration de fonction)
le calcul itératif (approche bottom-up avec ou sans recouvrement de la mémoire)
une approche matricielle basée sur l'exponentiation rapide de matrice
reprendre avec le schéma du TD de programmation \[\begin{cases} F_{2n}=F_n^2+F_{n-1}^2 & \\ F_{2n+1}= (2F_{n-1}+F_n)F_n& \end{cases}\]

Comment évolue la taille de \(F_n\) en fonction de \(n\) ? Quelles remarques peut-on faire sur la complexité du calcul ?

Introduction aux graphes (Mercredi 29 mai)

Une introduction aux graphes par Nadia Brauner, le vocabulaire, les propriétés, des raisonnements

Les transparents du cours slides

Les exercices feuille

et ne pas oublier le Cours ouvert de Graphe sur Caseine Cours

Expression des algorithmes (Lundi 24 avril)

Quelques remarques autour de l'expression des algorithmes Transparents

Apprentissage Par Problèmes (Lundi 24 avril + suite)

Les documents distribués :
- APP Généralités
- APP2: Hold'em for n00bs
Les documents supplémentaires :
- Greedy Algorithms
- Dynamic Programming

Diviser pour régner l'archétype du tri (Mardi 25/mercredi 26 juin)

À partir de l'analyse de deux algorithmes de tri, le tri partition/fusion et le tri par segmentation, on abordera le principe de diviser pour régner avec les schémas récursifs correspondants.

On reprend également le calcul de la complexité associée à de tels schémas Master Theorem

Feuille d'exercice avec des exercices avancés (les 3,4 et 5)

Pour réaliser la segmentation en place on utilise un algorithme dit du "drapeau hollandais", dû à Dijkstra ? (à confirmer) ou à Hoare (partition) Exemple du drapeau hollandais

Quelques compléments

Le texte de Hoare Communication of the ACM page 321

Comment "tuer" Quicksort A Killer Adversary for Quicksort

Les arbres (Jeudi 27 juin)

Introduction : qu'est-ce qu'un arbre ?

des racines, des branches, un tronc, des feuilles, ça grandit avec du soleil et du CO₂
une racine, des branches, des feuilles et c'est présent dans plein d'algorithmes

Un arbre n'est pas un objet natif en informatique. Ce n'est pas un type de base dans le matériel et très rarement dans les languages.

Un arbre est une structure pour stocker et/ou représenter de l'information, structure sur laquelle on pourra appliquer des algorithmes.

Avoir une structure générique permet de concevoir des algorithmes génériques s'appliquant à de nombreux problèmes différents.

Spécifications
- de l'objet lui-même
  - graphe sans cycle maximum en nombre d'arrête (avec un nœud racine)
  - Arbre := ArbreVide | (Étiquette, liste(Arbre))
    
    Ici, pas de distinction entre un arbre et un sous-arbre. C'est souvent une vision intéressante (appels récursifs facilités) mais parfois on a besoin de distinguer les deux notions.
- des accès
  - ListeFils(Arbre) -> liste(Arbre)
  - LectureEtiquette(Arbre) -> Étiquette
  - père(Arbre) -> Arbre
  - EstVide(Arbre) -> boolean
  - nbFils(Arbre) -> int
- de la construction de l'objet
  - construction fonctionnelle (sans effet de bord)
    - ArbreVide()
    - NouvelArbre(Étiquette, Arbre, Arbre) -> Arbre
  - construction avec effet de bord
    - ArbreVide()
    - AjouterFils(Arbre, Arbre) Le second arbre est ajouté à la liste des fils du premier

Propriétés

profondeur d'un nœud
- profondeur(n) = distance(n, racine)
hauteur d'un arbre
- hauteur(arbre) = max_{n ∈ arbre}(profondeur(nœud))
- par convention : hauteur(arbreVide) = -1
niveaux d'un arbre
- niveau(i, arbre) = { nœud ∈ arbre tq prof(nœud) == i }

Formes d'arbres

Arbres binaires et Arbres n-aires
Arbres binaires très utilisés en algorithmique, avec des spécifications adaptées :
- FilsGauche(Arbre) -> Arbre
- FilsDroit(Arbre) -> Arbre
- NouvelArbre(Etiquette, Arbre, Arbre) -> Arbre
peignes
- équivalent à une pile
- arbres binaires équilibrés
  - ∀ nœud ∈ arbre, |hauteur(filsDroit(nœud))-hauteur(filsGauche(nœud))| ≤ 1

Représentation des arbres

n-uplet
objet
tableau (chaînage par indice)

Algorithmes de parcours classiques

parcours en profondeur
- préfixé
- infixé exemple : Arbre Binaire de Recherche (ABR)
- posfixé exemple : calcul
Les trois en même temps : les appels de fonctions imbriquées (i.e. l'arbre d'exécution des fonctions d'un programme)

parcours_profondeur_recursif(arbre):
    traiter_prefixe(arbre)
    if non estArbreVide(fg(arbre)):
        parcours_profondeur_recursif(fg(arbre))
    traiter_infixe(arbre)
    if non estArbreVide(fd(arbre)):
        parcours_profondeur_recursif(fd(arbre))
    traiter_postfixe(arbre)

parcours_profondeur_prefixe(arbre):
  f = pileVide()
  enpiler(f, racine(arbre))
  while non pileEstVide(f):
      n = depiler(f)
      if non estArbreVide(n):
          traiter_prefix(n)
          enpiler(f, fg(n))
          enpiler(f, fd(n))

parcours en largeur utilisation d'une file.

En python, il faut utiliser un objet 'deque' qui permet des insertions/suppressions à l'un des deux bouts en temps constant. La liste classique permet l'insertion et la suppression en fin en temps constant, mais pas au début (coût linéaire). Or, pour une file, il faut enfiler à un bout et défiler à l'autre bout.

parcours_largeur(arbre):
  f = fileVide()
  enfiler(f, racine(arbre))
  while non fileEstVide(f):
      n = defiler(f)
      if non estArbreVide(n):
          traiter(n)
          enfiler(f, fg(n))
          enfiler(f, fd(n))

exercices :
- calcul de la hauteur d'un arbre binaire
- calcul du nombre de nœuds d'un arbre binaire
- calcul du nombre de feuilles d'un arbre binaire

Pour aller plus loin

Exercice présenté en cours : rotation d'un arbre
Exemple de feuilles d'exercices de troisième année de licence
- TD sur les arbres binaires :
  - manipulation d'arbres binaires avec une interface imposées
  Sujet, éléments de correction
- TD sur les arbres n-aires :
  - comment 'ranger' un arbre n-aire dans un arbre binaire
  - réflexions sur la différence entre la structure que l'on veut manipuler logiquement (l'arbre n-aire) et la structure dont on se sert pour la stocker (arbre binaire)
  Sujet, éléments de correction

Un peu de glouton (Lundi 1er juillet)

Les transparents et le problème de l'allocation d'intervalles (code illustratif, non optimisé) Le problème de l'arbre couvrant (feuille de TD) Quelques exercices de TD feuille de TD

Retour APP et QCM (Jeudi 4 juillet)

les transparents diffusés
le logiciel Auto Multiple Choice :
- Site web
- Le QCM généré (60 exemplaires avec permutation des réponses)
- Le code source LaTeX du QCM (les insertions d'image ont été commentées pour simplifier la compilation)
  
  Note : en commentant la ligne ,noshufflegroups (ligne 13) et la ligne \newpage (ligne 149), on obtient le même QCM avec :
  - permutation des groupes de questions
  - permutation des questions dans les groupes
  - mais le groupe "histoire" à la fin
  - et la question de la citation toujours en dernier

Activités d'informatique débranchée (Jeudi 4 juillet)

Point d'entrée possible pour ces activités :

plusieurs activités y sont directement proposées
des liens permettent de découvrir d'autres sites avec d'autres activités (et d'autres liens)
pour aller plus loin sur les marmottes aller voir le cours sur la compression du DU-ISN page

Recherche de motifs dans un texte (Vendredi 5 juillet)

Enveloppe convexe d'un nuage de points

Le problème : Étant donné un nuage de n points du plan, il faut construire l'enveloppe convexe de ces points, c'est à dire la séquence de points du nuage formant un polygone englobant l'ensemble du nuage.

En fait l'objectif pédagogique de la séance est de retrouver quelques schémas algorithmiques et de les adapter à un autre contexte. Nous n'avons détaillé que les algorithmes (pas de mise en oeuvre qui peut être faite par la suite)

On revient également sur la complexité de ces algorithmes et on révise des éléments de récursivité.

Algorithme de Jarvis (1973)

L'algorithme consiste à partir d'un point de l'enveloppe, par exemple celui d'ordonnée la plus faible puis à prendre la droite d'angle le plus faible avec les points restants

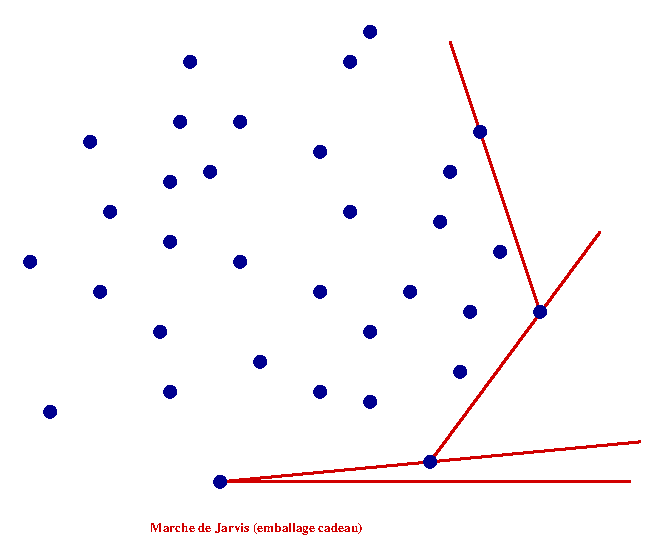
On évalue la complexité de cet algorithme (faire les calculs) à \(\mathcal{O}(n^2)\)

À quel schéma d'algorithme cela fait-il penser ? (tri par sélection)

Algorithme de Graham (1972)

L'algorithme consiste à partir d'un point intérieur (centre), on trie l'ensemble des points par angle croissant et on parcourt ces points dans l'ordre, le cas échéant, lorsque la convexité n'est pas respectée on se connecte au point précédentde l'enveloppe, par exemple celui d'ordonnée la plus faible puis à prendre la droite d'angle le plus faible avec les points restants

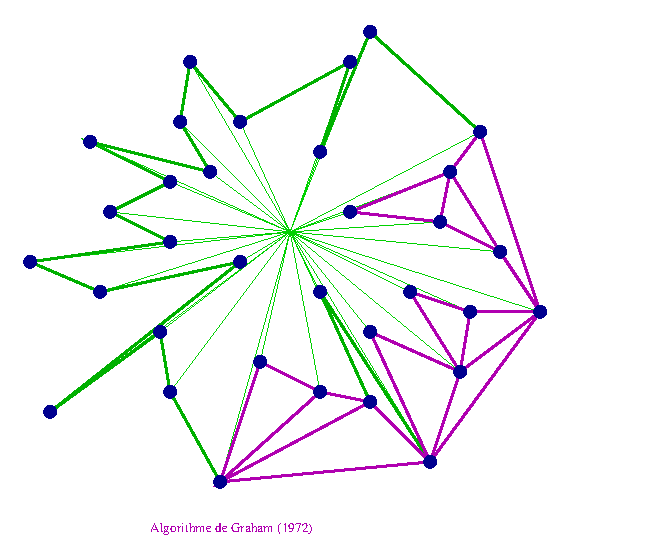
On évalue la complexité de cet algorithme (faire les calculs) à \(\mathcal{O}(n^2)\)

À quel schéma d'algorithme cela fait-il penser ? (tri par insertion)

Algorithme de partition-fusion

L'algorithme consiste à séparer par une droite le nuage de points en 2 nuages de points de même taille, on peut au préalable trier les points par abscisse croissante (coût en \(\mathcal{O}(n\log n)\)). On applique l'algorithmes aux deux sous-nuages, puis on recolle les 2 enveloppes obtenues en "remontant les tangentes" plus faible avec les points restants

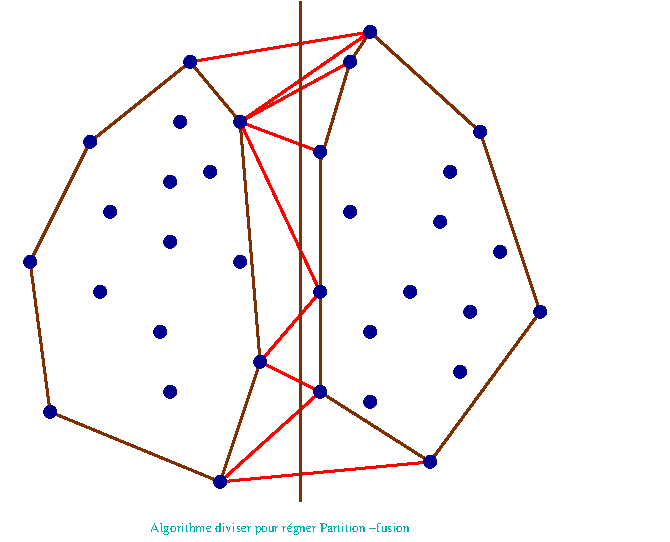
On évalue la complexité de cet algorithme (faire les calculs) à \(\mathcal{O}(n \log n)\)

À quel schéma d'algorithme cela fait-il penser ? (tri partition fusion)

Algorithme Quick-Hull

L'algorithme consiste à segmenter le nuage par un segment entre 2 points de l'enveloppe (ici les points de plus faible et plus grande abscisse). On traite indépendamment le nuage au dessus du segment et au-dessous du segmen. On prend le point le plus éloigné du segment(il est sur l'enveloppe) et on recommence.

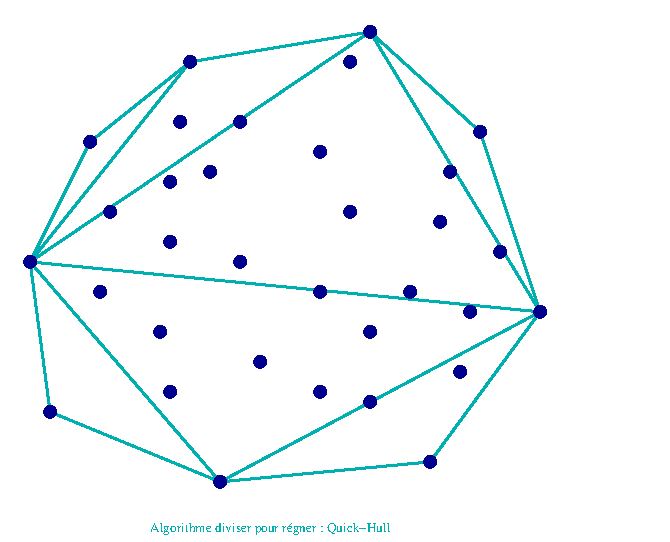
On évalue la complexité de cet algorithme (faire les calculs) à \(\mathcal{O}(n \log n)\) en moyenne

À quel schéma d'algorithme cela fait-il penser ? (tri par segmentation)

4 Quelques références bibliographiques

Attention cette bibliographie concerne la formation des enseignants et n'est pas destinée aux élèves de NSI, elle permet de prendre du recul par rapport au domaine et illustre des approches différentes de l'algorithmique. Des références historiques sont également fournies ainsi que des ouvrages plus "grand public".

Bibliographie

Pour aller plus loin le site Interstice contient une foule d'idées et de synthèses accessibles pour des élèves de lycée

Et pour la compréhension des liens entre informatique et société le Le blog binaire du Monde